logo Thorsten Pawletta, Hochschule Wismar - University of Technology, Business & Design

Belegarbeit


Thema: 

Entwicklung eines Simulationsprogramms zur Untersuchung einfachen Nickverhaltens bei Motorrädern

Eingereicht am:  29. November 1999
von: 
 Andreas Heim
Betreuer: 
 Prof. Dr.-Ing. T. Pawletta, Hochschule Wismar
Dr.rer. nat.  G. Sauerbier,  PNP-Luftfedersysteme GmbH Parchim

Problemstellung:

Gas-Feder-Dämpfer-Einheiten (GFD-Einheiten) zeichnen sich durch besonders günstige Federungs- sowie Dämpfungseigenschaften aus und werden heute vorallem in der Fahrzeugindustrie eingesetzt. Ihre Konstruktion ist jedoch relativ aufwendig. Um die Anzahl der nötigen Konstruktionsschritte vom ersten Prototypen bis hin zum optimal abgestimmten Gas-Feder-Dämpfer zu verringern ist es sinnvoll, das Schwingungsverhalten des Fahrzeuges zuvor auf einem Rechner zu simulieren.
In dieser Arbeit wird das Schwingungsverhalten und speziell das Nickverhalten eines Motorrades numerisch untersucht. Zur Lösung des die Dynamik beschreibenden Differentialgleichungssystems wird ein spezielles Simulationsprogramm entwickelt.
Weiterhin wird eine graphische Benutzeroberfläche entworfen. Diese soll es ermöglichen, alle relevanten Parameter für die Simulation schnell und ohne großen Aufwand zu variieren. Neben einer numerischen Ergebnisausgabe wird eine Animationskomponente entwickelt, welche die wesentlichen dynamischen Eigenschaften anschaulich wiederspiegeln soll.
Die Implementation erfolgt mit dem wissenschaftlich- technischen Entwicklungssystem MATLAB.
 
 

Allgemeines Schwingungssystem:

Der Aufbau und die Massenverteilung eines Motorrades sind viel zu komplex, als dass sein Schwingungsverhalten genau berechnet werden könnte. Das Motorrad muss zur Berechnung in ein einfacheres Modell umgewandelt werden, das jedoch sein Schwingungsverhalten hinreichend genau nachbildet. Es ergibt sich das folgende vereinfachte Schwingungsmodell:

Schwingmodel

Die Massen m1, m2 und mk ersetzen die Aufbaumasse des Motorrades und werden als Punktmassen idealisiert. Die Masse mk ist die Koppelmasse. Sie liegt im Schwerpunkt des Systems und ist nötig, um den Energieaustausch zwischen den Massen m1 und m2 im Berechnungsmodell zu ermöglichen. Die Massen mr1 und mr2 ersetzen die Massen der Räder. Daraus ergibt sich ein Schwingungssystem mit vier Freiheitsgraden.
Das modellbeschreibende Differentialgleichungssystem lautet in Matrixschreibweise:

Matrix1Matrix2Matrix3
 

Dieses Differentialgleichungssystem 2.Ordnung muss in ein Differentialgleichungssystem 1. Ordnung überführt werden, um es mit den in MATLAB vorhandenen ODE-Solvern numerisch lösen zu können. Mit den Substitutionen:

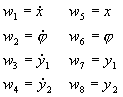
Substitution

ergibt sich:

Matrix4Matrix5
 

Dieses Differentialgleichungssystem kann in MATLAB numerischem effizient gelöst werden.

Das Motorrad überfährt ein Straßenprofil, welches in einem ASCII-Datenfile vorher vereinbart worden ist. Dieses Datenfile kann eine einfache Sinusschwingung oder ein reales auf der Straße gemessenes Profil enthalten. Die Form der Erregung des Systems kann beliebig gestaltet werden. Die Erregungsdaten werden dem Simulationsprogramm in Form eines ASCII-Datenfiles übergeben. Das Daten-File enthält Informationen über den Weg und das über den Weg aufgetragene Profil der Erregung. Aus der Länge des Motorrades und der Fahrgeschwindigkeit ergeben sich dann die entsprechenden Amplituden der Erregung am Vorder- und Hinterrad.
 
 

Das Simulationsprogramm:

Das Simulationsprogramm besteht aus den folgenden Programmkomponenten:
 
Steuerprogramm (Hauptprogramm) (Simulator.m)
Modell-File (ODE-File) (odef.m)
DGL-Löser (ODE-Solver) (ode45.m)
Animationsprogramm (animation.m)
Graphisches Nutzer-Interface (simul.m, simul.mat)

Die folgende Tabelle zeigt die prinzipiellen Aufgaben der einzelnen Komponenten des Simulationsprogramms.

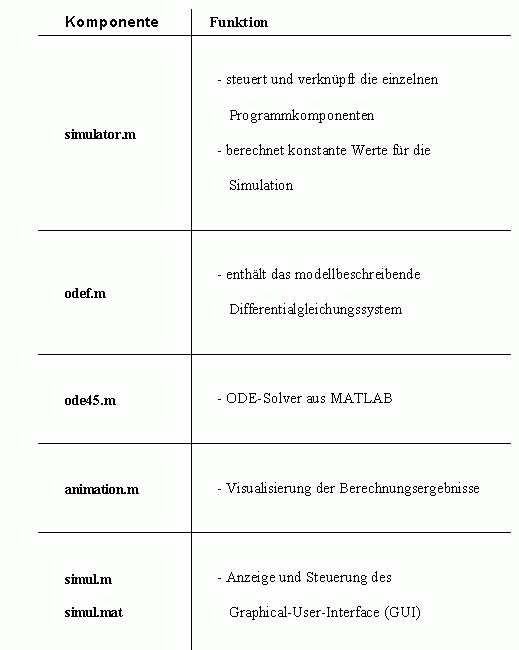
Tabelle1
 
 

Experimente:

Das Schwingungsmodell wurde mit einer Reihe von Testfunktionen angeregt, um die Berechnungsergebnisse mit den praktisch vorliegenden Erfahrungen zu vergleichen. In der unteren Abbildung sind beispielhaft die Ergebnisse aus der Simulation beim Überfahren eines rampenförmigen Straßenprofils dargestellt.

Experimente1

Die Simulationsergebnisse aus den durchgeführten Experimenten entsprachen den Erwartungen und haben gezeigt, dass das Simulationsprogramm richtig arbeitet.
 

Zusammenfassung/Ausblick:

In dieser Arbeit ist ein Berechnungs- und Simulationsprogramm zur Untersuchung des Schwingungsverhaltens eines Motorrades entwickelt worden. Hierbei wurden bei der Modellbildung teilweise sehr starke Vereinfachungen vorgenommen. In das Simulationsprogramm wurde die Möglichkeit einer beliebigen zeitlich nicht konstanten Erregung eingebracht. Dadurch ist es u.a. möglich, unter realen Bedingungen gemessene Straßenprofile in die Simulation einfließen zu lassen. Des weiteren fließen auch die Einflüsse der Bereifung auf das Schwingungsverhalten des Fahrzeuges in die Simulation ein. Dies ist für die konkrete Abstimmung eines Feder-Dämpfer-Systems in einem Fahrzeug von großer Bedeutung.

Die Eigenschaften der im Berechnungsmodell verwendeten Federn und Dämpfer sind über den Hubweg als konstant vorausgesetzt. Dies trifft in der Realität meist nicht zu. Es ist für die Simulation günstiger, wenn ein bestimmtes Eigenschaftsprofil für die Federn und Dämpfer über den Hubweg vorgegeben werden kann. Es ist ebenfalls denkbar, für die Feder- und Dämpferelemente Differentialgleichungen in das modellbeschreibende Differentialgleichungssystem einzuführen, die ihre Eigenschaften besser beschreibenden. Durch eine solche Erweiterung des Simulationsprogramms könnten sogar die komplexen Eigenschaften der GFD-Einheiten direkt in das Berechnungsmodell einfließen. Dadurch wäre es möglich, das Schwingungsverhalten des Systems unter Verwendung von GFD-Einheiten als Feder-Dämpfer-Elemente zu untersuchen.

Als weiterer Ausblick ist noch die Erweiterung des Berechnungsmodells auf ein räumliches System zu sehen. D.h. dem Berechnungsmodell wird ein zusätzlicher Freiheitsgrad hinzugefügt, nämlich eine Drehung um seine Längsachse. Dies würde auch die Untersuchung des Schwingungsverhaltens von Pkws ermöglichen.

Andreas Heim

E-Mail: an.heim@web.de